PaizaのスキルチェックのAランクの問題をすべて解きました。
(2023/01/30時点で全52問「細長い国」まで)
もちろん問題の内容をお教えすることはできませんが、Aランクで戦うのにどのようなアルゴリズムの知識が必要かについて紹介できればと思います。
Aランクの問題は愚直に実装すると大規模データで必ずタイムアウトしてしまいます。
正しいアルゴリズムを知っていないと一生解けないという問題もないこともないように感じます。
どうぞこちらでアルゴリズムの知識を得ていってくれればと思います。
例文はC#にて書いております。
まずはどのようなものを参考にしてアルゴリズムの勉強をしたかを紹介します。
そのあとAランク問題を解くのに必要になるであろうアルゴリズムをいくつか紹介します。
参考にしたもの
プログラミングコンテスト攻略のためのデータ構造とアルゴリズム
スタック・キューや探索、再帰関数などの知識などはこの辺りの参考書を読むとよいかと思います。
競技プログラミングの鉄則
初心者向けの本になると思います。
動的計画法など競技プログラミング必須のアルゴリズムが紹介されています。
内容としては下の競プロ典型90問と被る部分もありますので無料で進めたい場合はまずAtCoderからやってみるとよいかと思います。
AtCoder 競プロ典型90問
AtCoderの問題は解いた方々の解答を観ることができるのでとても有意義です。
なかでも競プロ典型90問は作問者の方がTwitterで解説もしてくれているのでとても勉強になります。
難易度4から5程度までが解けるようになればPaiza Aランクで十分通用すると思います。
E869120さんという方が解説してくださっています。
他のツイートで流れたりしててこのツイートにたどり着くの意外と大変なのでリンクを張っておきますね
知っておきたいデータ構造・アルゴリズム
スタック・キュー
スタックは先入れ後出し。後に入れたデータほど先に取り出すことができます。
キューは先入れ先出し。先に入れたデータを先に取り出すことができます。
スタックとキューは深さ優先探索、幅優先探索で用いることが多いです。
深さ優先探索はスタック、幅優先探索はキューを用います。
StackはPush()関数でデータ格納、Pop()関数でデータ取り出し。
QueueはEnqueue()関数でデータ格納、Dequeue()関数でデータ取り出しになります。
スタックは逆ポーランド記法や最大長方形探索の実装などにも用います。
変数の型(int, longの使い分け)
競技プログラミングにおいては基本的に整数を使うことが多いと思いますが、
普段何気なく使っているintは32ビット整数で、その範囲は-2147483648~2147483647になります。
問題の種類によってはこの値を超える可能性があります。
その場合intではオーバーフローを起こして問題に不正解になってしまいます。
そうならないように64bit整数のlongを使いましょう。
そこまでメモリにシビアになることもないかとは思いますので、基本迷ったらlongでいいかなとは思います。
ハッシュセット
数字を格納しておきたいけど、重複する数字を入れたくない。
そのようなときはハッシュセットを使うとよいです。
C#ではHashSetクラスになります。
例えばリストとハッシュセットに1を2回格納する場合
リストには1が2個、ハッシュセットには1が1個格納されます。
List<int> list = new List<int>();
list.Add(1);
list.Add(1);// 1が2個格納される
HashSet<int> hashset = new HashSet<int>();
hashset.Add(1);
hashset.Add(1);// 1が1個格納される幅優先探索・深さ優先探索
探索は競技プログラミングに必須の能力になるかと思われます。
探索には大きく深さ優先探索(Depth First Search)と幅優先探索(Breadth First Search)の2種類があります。
深さ優先探索は見つかった点を次々進んでいき、幅優先探索は現在の点の周りの点をすべて回ってからさらに次に進んでいきます。
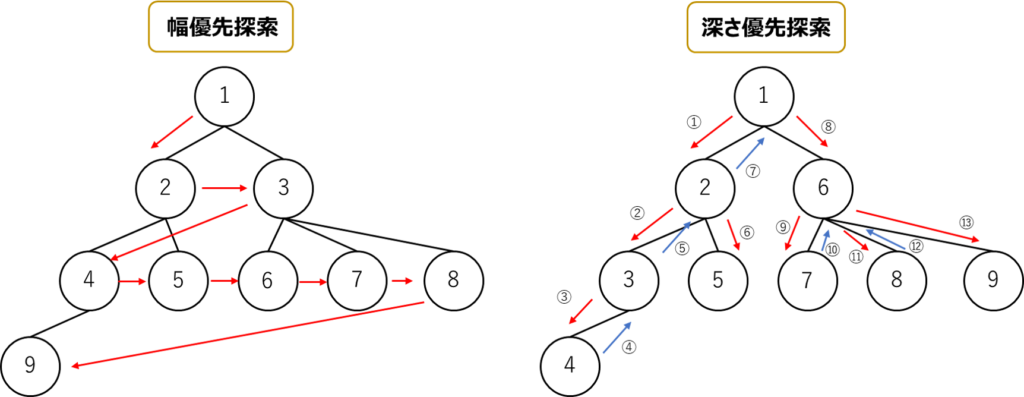
深さ優先探索はスタックもしくは再帰関数で実装します。一方幅優先探索はキューで実装します。
基本的に迷路のようなスタート位置からゴール位置を探索するような問題では深さ優先探索でも幅優先探索でもほとんど変わりません。
しかし深さ優先探索と幅優先探索の違いを理解しておくことはとても大切です!
幅優先探索は最も近い点、条件を満たす最小回数など最小を求められた場合に使用されます。
例えば迷路においてスタート地点から最小何手で出口にたどり着けるかを求めるとします。
このような場合はキューに迷路の現在位置と移動回数を格納します。
幅優先探索はスタート地点からじわじわと探索範囲を広げていくイメージです。
探索は移動回数の少ないところから順にキューから取り出されていきますので、出口が見つかったタイミングで探索を終了し、その時の移動回数が最小値となります。
答えが見つかった時点で探索を打ち切ってよく、そのときの値が答えになる。
それが幅優先探索のイメージです。
反対に深さ優先探索は複数の可能性を列挙する必要がある場合などに使います。
例えばスタート地点からいくつかの点を経由してスタート地点に戻ってくるときの移動コストを列挙したい場合などは深さ優先探索です。
このような場合はスタックに現在地点とこれまでの移動コストを格納します(後ろに戻らないなどの条件を足す場合はどの地点から来たかの情報も記憶しておく必要があります)
深さ優先探索はどんどんと先に進んでいく探索です。
見つかった隣接点にどんどん進んでいきスタート地点に戻ったらそのときのコストを保存します。
探索が進むにつれてどんどんスタート地点に戻ってきたときのコストが格納されていくことになります。(ここでの説明は少し簡略化しています。適当に実装すると一生ぐるぐる回り続けて探索が終わらなかったりするので最大コストで探索を終了することや、一度通ったシチュエーションは探索しないなどの工夫が必要です)
少し複雑だったかもしれませんが深さ優先探索と幅優先探索を使い分けれるようになるとかなり問題を解く力が向上すると思います。
分枝限定
上の項で探索の話をしましたが、探索を効率よく行うことはとても重要です。
例えば迷路においては一度探索したところは探索しない、コストのあるグラフにおいては現在のコストと比較して大きいか・小さいかなどのがあるかと思います。
このような条件をつけ足し忘れていると探索が永遠に終わらないなどの問題にぶち当たってしまいます。この辺りは慣れという部分も少しあるとは思いますが意識してみてもらえればと思います。
動的計画法
動的計画法も競技プログラミングにおいての必須テクニックです。
ナップザック問題などの典型的な問題も動的計画法の一種です。
動的計画法は本当に様々な用途で使用されます。
愚直なやり方でタイムアウトした問題は、よくよく考えてみたら動的計画法で解けたということを私はかなり経験しています。
動的計画法の種類は本当に多岐にわたります。
鉄則本がかなり参考になるかと思います。
動的計画の判断のポイントは
・時系列やステップが進んでいく
・選択肢の中からいくつかを選んで最適を目指す
といった内容であるかどうかだと思います。
x歩とy歩飛ばしで飛び石を渡るときi番目の飛び石を踏むことができますか?数字の書かれたカードから何枚かを選んでその和をSにできますか?などだと思います。
UnionFind
UnionFindは重複の無い数字をグループ分けした後、
グループに属している数字の個数・2つの数字が同じグループに属しているかを高速に判定することのできるアルゴリズムです。
数字がどんどん連結していくようなイメージのときはUnionFindを使います。
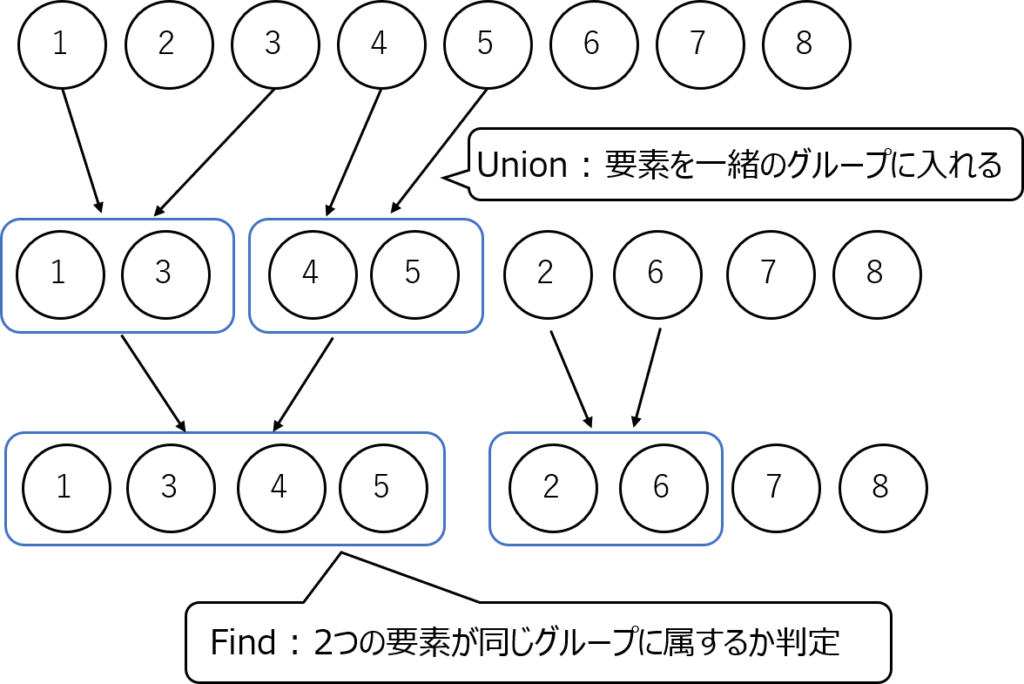
例えば複数の人がいたとして各々自由に動き回り、2人の人が出会うとじゃんけんをして負けた人は勝った人の手下になるみたいなゲームを考えます。(負けた人の手下も勝った人の手下になります。じゃんけん列車というそうです。子供のころやった気がします)
このような場合はUnionFindが使えます。
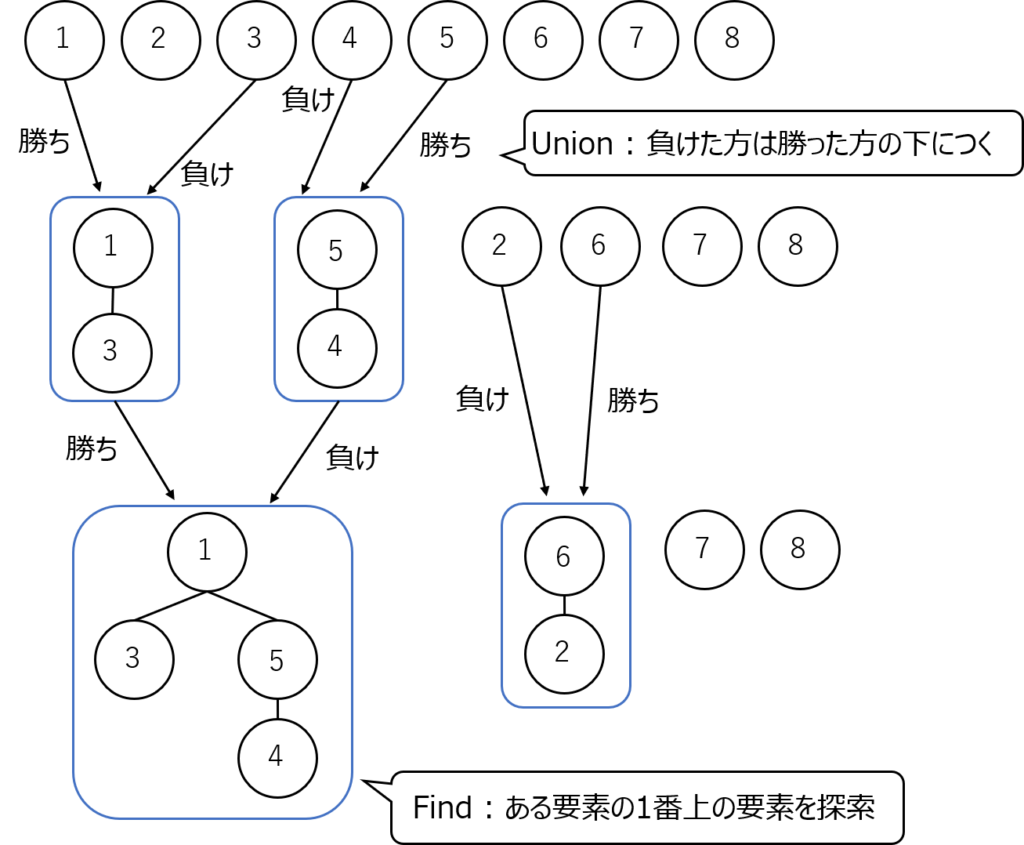
勝った人と負けた人のグループをunion()関数で合併し、find()関数である人の一番先頭の人を見つけます。
実装は以下のようになります。
public class UnionFind
{
// 親要素のインデックスを保持する
// 親要素が存在しない(自身がルートである)とき、マイナスでグループの要素数を持つ
public int[] Parents { get; set; }
public UnionFind(int n)
{
this.Parents = new int[n];
for (int i = 0; i < n; i++)
{
// 初期状態ではそれぞれが別のグループ(ルートは自分自身)
// ルートなのでマイナスで要素数(1個)を保持する
this.Parents[i] = -1;
}
}
// 要素xのルート要素はどれか
public int Find(int x)
{
// 親がマイナスの場合は自分自身がルート
if (this.Parents[x] < 0) return x;
// ルートが見つかるまで再帰的に探す
// 見つかったルートにつなぎかえる
this.Parents[x] = Find(this.Parents[x]);
return this.Parents[x];
}
// 要素xの属するグループの要素数を取得する
public int Size(int x)
{
// ルート要素を取得して、サイズを取得して返す
return -this.Parents[this.Find(x)];
}
// 要素x, yが同じグループかどうか判定する
public bool Same(int x, int y)
{
return this.Find(x) == this.Find(y);
}
// 要素x, yが属するグループを同じグループにまとめる
public bool Union(int x, int y)
{
// x, y のルート
x = this.Find(x);
y = this.Find(y);
// すでに同じグループの場合処理しない
if (x == y) return false;
// xの方をルートにする合併
// まとめる先のグループの要素数を更新
this.Parents[x] += this.Parents[y];
// まとめられるグループのルートの親を書き換え
this.Parents[y] = x;
return true;
}
}使用する際はコンストラクタの引数に要素数を渡します。
UnionFind uf = new UnionFind(N);合併する際はUnion()関数、ルートを探す際はFind()を用います。
// Union
uf.Union(1, 2);
// Find
uf.Find(2);累積和
累積和とは、数列においてその順にその和をとっていった数列になります。

累積和の知識を用いれば、数列におけるある区間の和を高速に求めることができます。
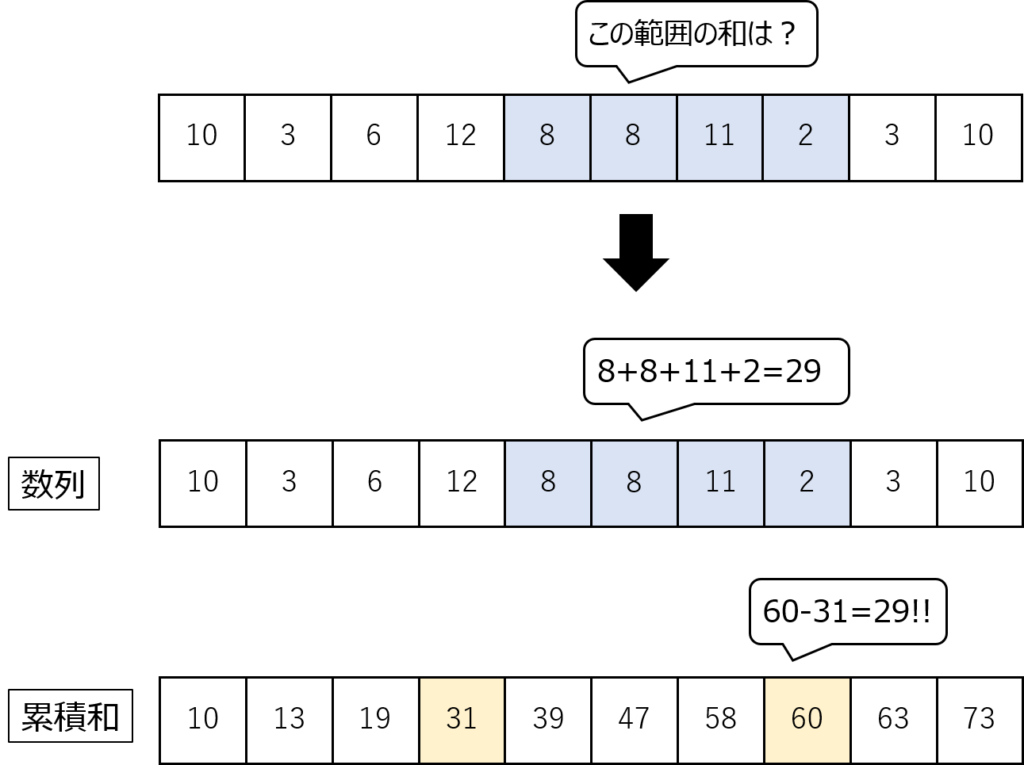
例えば上の図において5番目から8番目の要素の和を求めたいとします。
単純に考えれば8+8+11+2=29となります。
しかしあらかじめ累積和を求めておけば4番目までの要素の和と8番目の要素の和の差を求めることで答えが求まります(60-31 = 29)。
わざわざ必要な要素を1つずつ足すことなく、引き算1回で答えが求まるようになります。
このようにあらかじめ累積和を計算しておくことによりプログラムの速度が改善します。
いもす法
いもす法は累積和の知識を応用した数直線や平面上での最大値を求めるテクニックです。
以下の図のような一本道に街灯があるような状況を考えましょう。
それぞれの街灯は照らせる範囲が異なっています。
このような状況で一番多くの街灯に照らされている地点を求めます。
いもす法では開始点と終了点に着目します。
開始点で+1、終了点で-1をし、それの累積和を求めます。
その求めた累積和がその地点において街灯が当たっている数に相当します。
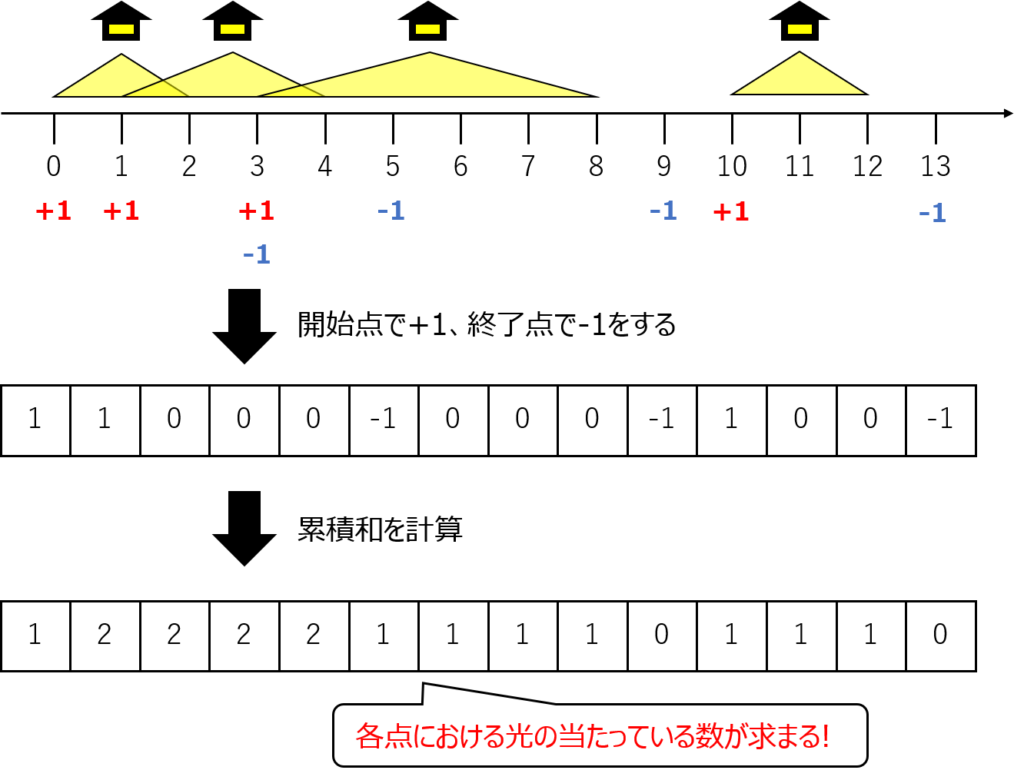
街灯が当たっている地点が分かるので、最も長く街灯が当たっている区間を求めることもできます。
いもす法は2次元にも対応できます。
2次元でのいもす法は平面の左上と右下で+1、右上と左下で-1をした後、行方向で累積和をして列方向に累積和を求めます。
机の上の好きな場所に紙をどんどんおいていくとして、一番紙が重なっているところは何枚紙が重なっているかを求めるときなどはいもす法が有効です。
(紙を置くたびにその範囲の配列を+1しているとタイムオーバーします。いもす法は四隅だけ+1か-1するので高速化が可能です)
LowerBound
LowerBoundとは昇順で並んでいる数列において、ある数字がその数列において何番目の大きさになるかを求めるものです。
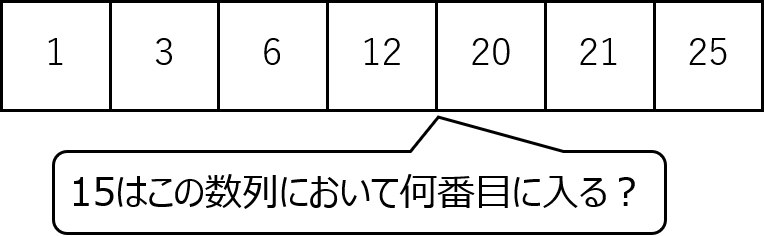
コードは以下になります。
public int LowerBound(int[] arr, int val)
{
int low = 0, high = arr.Length;
int mid;
while (low < high)
{
mid = ((high - low) >> 1) + low;
if (arr[mid] < val) low = mid + 1;
else high = mid;
}
return low;
}このテクニックはある数字より小さい要素の数を求めたり、座標圧縮というアルゴリズムにて使用します。(数字そのものではなく、数字が数列の中で何番目に大きいかを保持するという考え方です)
尺取り法
尺取り法は数列においてある範囲を調べたいときに使用されるテクニックです。
調べる範囲の開始地点と終了地点が尺取り虫の動きのように進んでいくのでこう呼ばれています。
それでは例題を考えてみましょう。
以下の図のような問題を考えてみましょう。
あるレッスン教室では①から④のレッスンが受けられます。
ケチなAさんはできるだけ払う会費を少なくできるように最短ですべてのレッスンを受けることのできる日程を探しています。そのような日程を求めてください。

愚直に考えると開始地点を定めてそこからすべてのレッスンを受けれるまでの日数を求めればよいかと思われます。
しかしこれでは日程が長い場合は時間がかかりすぎてしまいます。
そこで用いられるアルゴリズムが尺取り法です。
まずは全てのレッスンを含むようになるまで最初の点から日程を進めていきます。
この時点で最小値の候補は7になります。

すべてのレッスンを含む日程が見つかったら次はどれかのレッスンが含まれなくなるまで日程の開始地点を進めていきます。
開始地点を進めていく途中ですべてのレッスンを含む日程の最小値が更新される場合は答えを更新します。
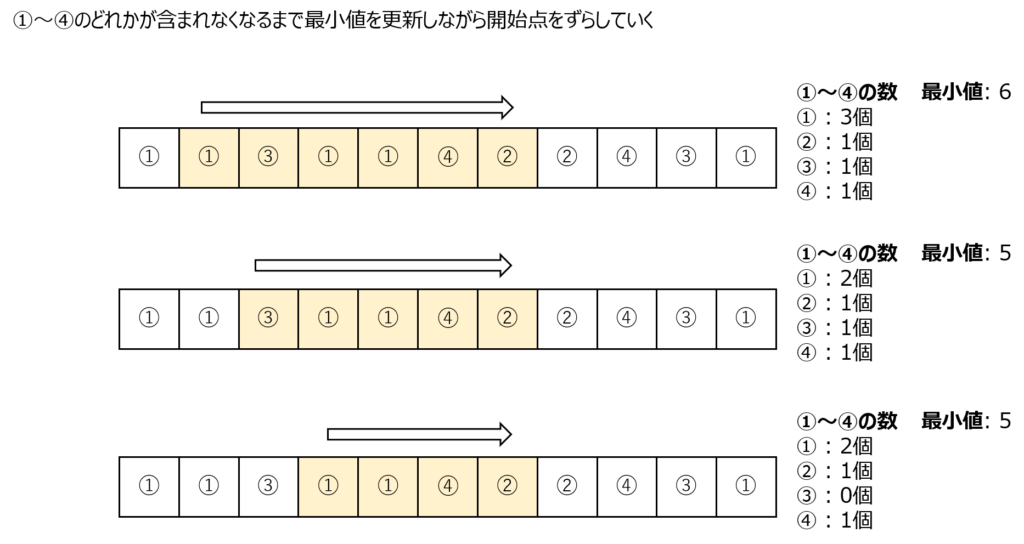
どれかのレッスンが含まれなくなったら次は再びすべてのレッスンが含まれるように終了地点を進めていきます。
そしてすべてのレッスンが含まれたらどれかのレッスンが含まれなくなるまで開始地点を進めていく。というように開始地点と終了地点を交互に進めていきます。(確かに尺取り虫みたいな動きですよね)
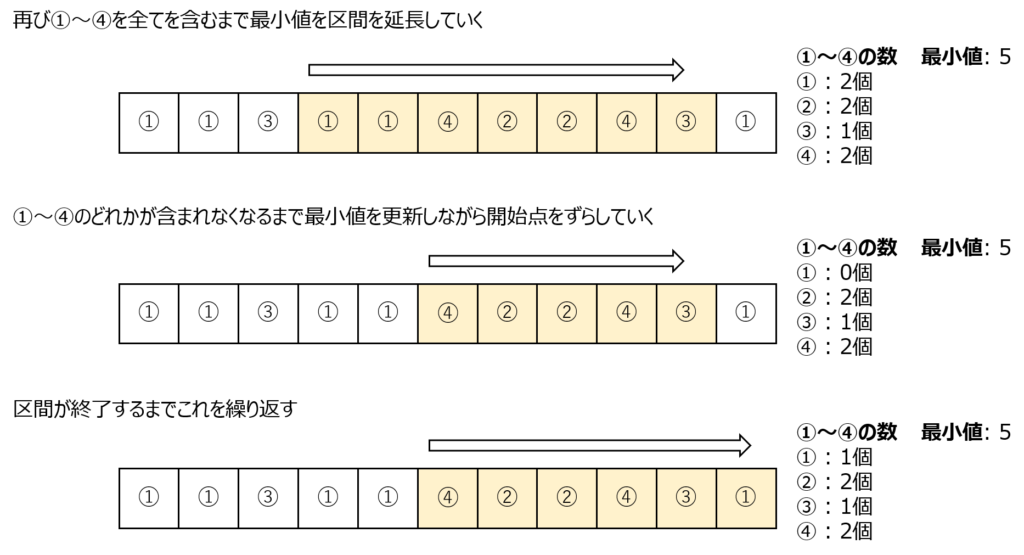
このアルゴリズムを使えば高速に全ての日程を走査することができます。
コードは以下のようになります。ご参考にしてくださればと思います。
// 尺取り法
// 種類がNになるまで進む
// sche : 日程。ここにどのレッスンかの情報が格納されているとします。
// num[] : 見ている範囲におけるレッスンの数
// length : 見ている範囲の長さ
// types : 見ている範囲内のレッスンの種類数
foreach (int a in sche)
{
que.Enqueue(a);
if (num[a] == 0)
{
types++;
length++;
num[a]++;
}
else
{
length++;
num[a]++;
}
while (types == N)
{
// Nに到達したら先頭側から削っていく
ans = Math.Min(ans, length);
int n = que.Dequeue();
num[n]--;
length--;
if (num[n] == 0)
{
types--;
break;
}
}
}外積
幾何問題を考える際には外積の知識があると問題を楽に解けることがあります。
外積を用いることで平面上のある点が、ある直線より上に位置するか下に位置するかを判定することができます。
例えば点\( (x_2, y_2)\) が、\( (x_0, y_0)\) と\( (x_1, y_1)\) を結ぶ直線より上にあるか、下にあるか。これを求めたいとします。
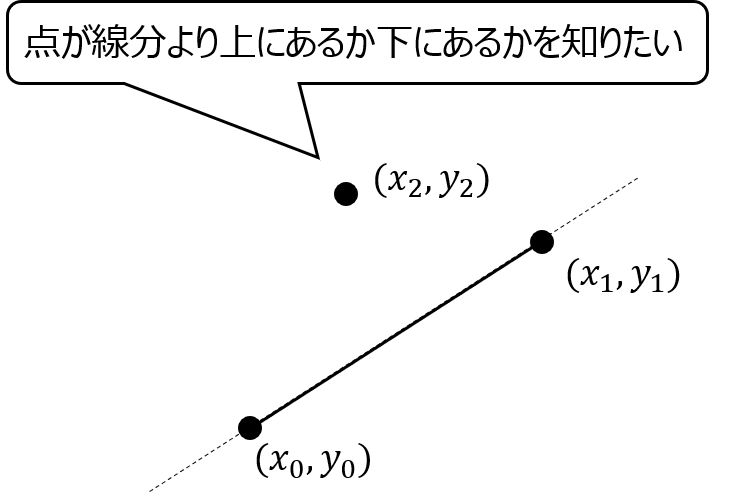
外積を用いてこの問題を解く際には\( (x_0, y_0)\)から\( (x_1, y_1)\)、\( (x_0, y_0)\)から\( (x_2, y_2)\)を結ぶベクトルをまず考えます。
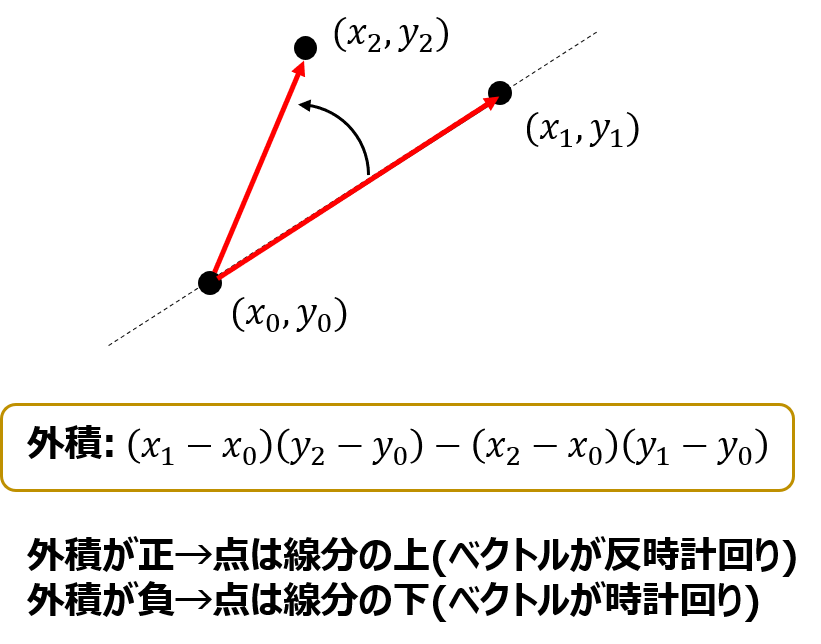
そしてこの2つのベクトルの外積を求め、その正負で判定を行います。
このとき外積は\( (x_1 – x_0)(y_2 – y_0)-(x_2 – x_0)(y_1 – y_0)\)となります。
そしてこの外積の値が正であればベクトルは反時計回り、つまり点は直線の上にあるということになります。
これを応用することで平面上の点が三角形の中にあるかどうか、扇形の中にあるかどうかを判別できます。
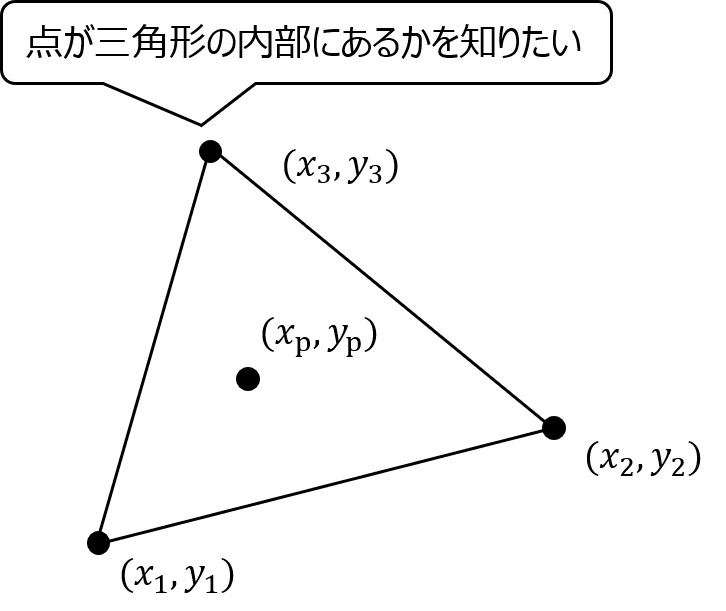
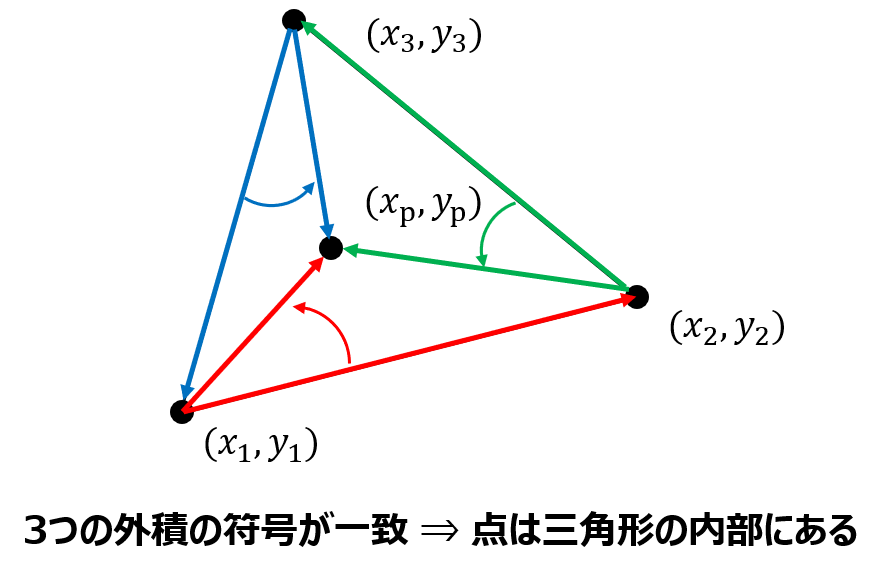
各頂点から他の頂点へのベクトルと、頂点から点へのベクトルとの外積を3つ求めます。
そしてその外積の正負が一致すれば点は三角形の内部にあると判断できます。
扇形の場合も外積が利用できます。
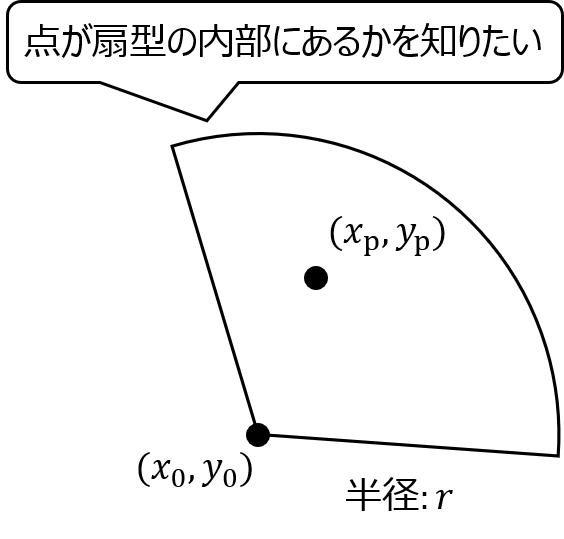
扇形の場合は辺のベクトルと中心から点へのベクトルの外積と、中心から点への距離が扇の半径より小さいかで判断できます。
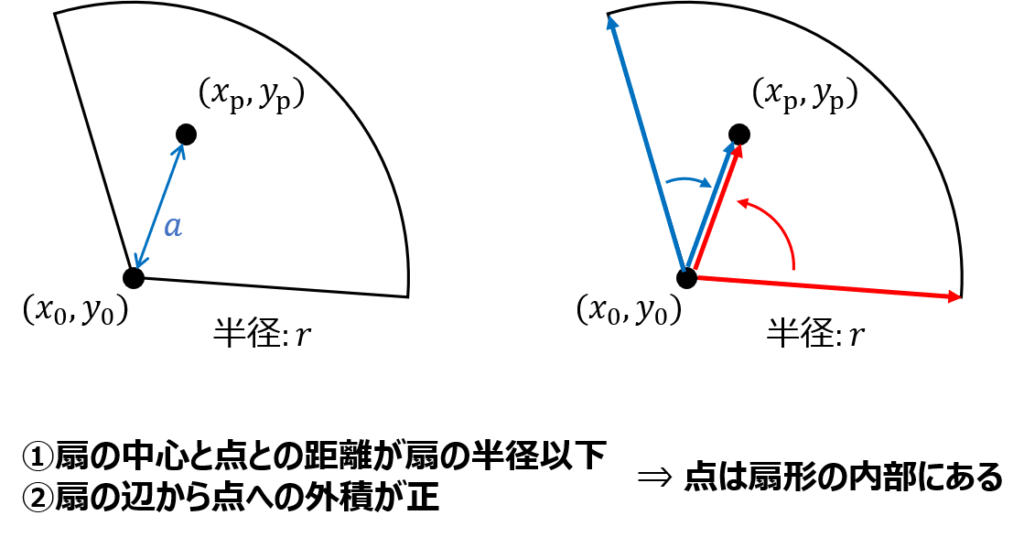
このように幾何問題において外積は大きな力を発揮します。
二部グラフ
二部グラフとはグラフにおいて頂点を2つにグループ分けでき、それぞれのグループの頂点は同じグループの頂点とはつながっていないグラフのことです。
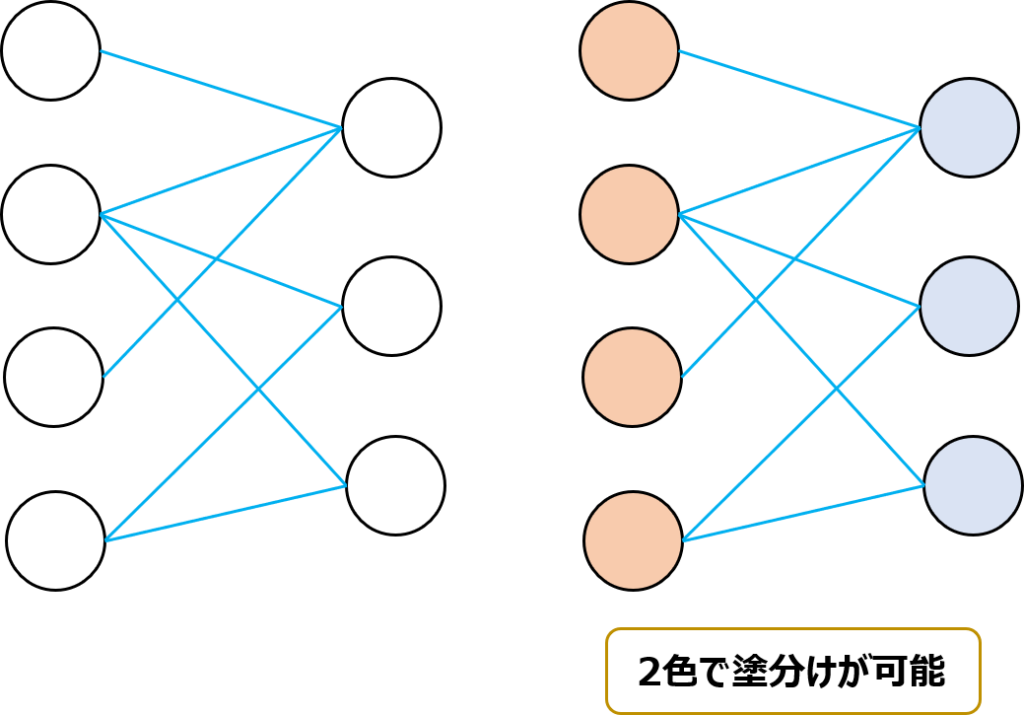
以下の図は二部グラフの例になります。頂点を2つのグループに分けることができており、かつどちらのグループの頂点も同じグループの頂点とはつながっていません。
二部グラフの特徴は2色で塗分けが可能ということです。
この知識はグラフの彩色問題で役に立つかと思われます。
二部グラフの判定は探索で行うことができます。
まず任意の点を便宜的に1つの色であるとします。そして探索を行い、隣り合う色を別の色で塗ります。探索中にすでに色が塗られている点を見つけたとき、その色が今の点の色と同じであるときに二部グラフではないと判断できます。
最後に
長かったですがここまでお読みいただきありがとうございます。
上記のアルゴリズムの知識があれば問題を解くのがかなり楽になると思います。
参考になりましたら幸いです。



コメント